목차
문제
<1로 만들기>
- 정수 X가 주어졌을 때, 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지입니다.
- X가 5로 나누어 떨어지면, 5로 나눕니다.
- X가 3으로 나누어 떨어지면 3으로 나눕니다.
- X가 2로 나누어 떨어지면, 2로 나눕니다.
- X에서 1을 뺍니다
- 정수 X가 주어졌을 때, 연산 4개를 적절히 사용해서 값을 1로 만들고자 합니다. 연산을 사용하는 횟수의 최솟값을 출력하세요.
예를 들어 정수가 26이면 다음과 같이 계산해서 3번의 연산이 최솟값입니다.
- 26 -> 25 -> 5 -> 1

이 문제는 피보나치 수열과 마찬가지로 함수가 호출되는 과정을 그림으로 보면 최적 부분 구조와 중복되는 부분 문제를 만족한다.

점화식을 작성해보면

위와 같이 나올 수 있다.
단, 1을 빼는 연산을 제외하고는 해당 수로 나누어떨어질 때에 한해 점화식을 적용할 수 있다.
답안
x = int(input())
d = [0] * 30001
for i in range(2, x+1):
# 현재의 수에서 1을 빼는 경우
d[i] = d[i-1] + 1
# 현재의 수가 2로 나누어 떨어지는 경우
if i % 2 == 0:
d[i] = min(d[i], d[i//2] + 1)
# 현재의 수가 3으로 나누어 떨어지는 경우
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)
# 현재의 수가 5로 나누어 떨어지는 경우
if i % 5 == 0:
d[i] = min(d[i], d[i//5] + 1)
print(d[x])'알고리즘' 카테고리의 다른 글
| Dynamic Programming #2 (문제풀이 1) (0) | 2023.10.09 |
|---|---|
| Dynamic Programming #1 (0) | 2023.10.09 |
| 백준 1918 (후위 표기식) (0) | 2023.08.17 |
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
목차
문제
개미 전사는 메뚜기 마을의 식량창고를 몰래 공격하려고 합니다. 메뚜기 마을에는 여러개의 식량창고가 있는데 식량창고는 일직선으로 되어 있습니다
각 식량창고에는 정해진 수의 식량을 저장하고 있으며 개미 전사는 식량창고를 선택적으로 약탈하여 식량을 빼앗을 예정입니다.
이때 메뚜기 정찰병은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량창고가 공격받으면 알아챌 수 있습니다.
따라서 개미 전사가 정찰병에게 들키지 않고 식량창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량창고를 약탈해야 합니다.
개미 전사는 식량창고 N에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최댓값을 구하는 프로그램을 작성하시오.
예를 들어 식량창과 4개가 있다고 가정하자.
{1, 3, 1, 5}
그렇다면 개미전사는 두번째와 4번째 식량창고를 털었을때 총합 8로 최대 식량을 얻을 수 있다.

동적프로그래밍의 메모이제이션을 활용하여 풀어보자.
왼쪽부터 차례대로 식량창고를 턴다고 했을 때, 마지막 식량창고를 털지 안털지 유무에 따라 2가지로 나눌 수 있다.
마지막 식량창고를 털면 바로 전 식량창고는 못털게 되고,
마지막 식량창고를 털지 않으면 바로 전 식량창고를 털 수 있다.


일때 점화식을 작성해보면
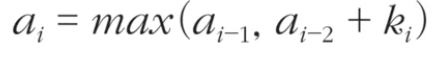
위와같은 식이 나오게 된다. 여기서 한 칸 이상 떨어진 식량창고는 항상 털 수 있으므로 (i-3)번째 이하는 고려할 필요가 없다.
답안
n = int(input())
# 모든 식량 정보 입력 받기
array = list(map(int, input().split()))
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100
# 다이나믹 프로그래밍 진행 (bottom - up)
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
d[i] = max(d[i-1], d[i-2] + array[i])
print(d[n-1])
'알고리즘' 카테고리의 다른 글
| Dynamic Programming #3 (문제풀이 2) (0) | 2023.10.11 |
|---|---|
| Dynamic Programming #1 (0) | 2023.10.09 |
| 백준 1918 (후위 표기식) (0) | 2023.08.17 |
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
목차
Dynamic Programming
- 다이나믹 프로그래밍은 동적 계획법이라고도 부른다.
- 일반적인 프로그래밍 분야에서 말하는 동적(Dynamic)는 프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법을 의미한 다.
- 반면에 다이나믹 프로그래밍에서 "Dynamic"은 별다른 의미없이 사용된 단어이다.
다이나믹 프로그래밍은 문제가 다음의 조건을 만족할 때 사용할 수 있다.
1. 최적 부분 구조 (Optimal Subtructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
2. 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야 한다.
메모이제이션 (Memoization)
- 메모이제이션은 다이나믹 프로그래밍을 구현하는 방법 중 하나이다.
- 한 번 계산한 결과를 메모리 공간에 메모하는 기법이다.
- 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져온다.
- 값을 기록해 놓는다는 점에서 캐싱(Chching)라고도 한다.
Top-Down VS Bottom-Up
- top-down 방식은 하향식이라고도 하며, bottom-up 방식은 상향식이라고도 한다.
- 다이나믹 프로그래밍의 전형적인 형태는 bottom-up 방식이다.
- 결과 저장용 리스트는 DP 테이블이라고 부른다.
- 엄밀히 말하면 메모리제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미한다.
- 따라서 메모이제이션은 다이나믹 프로그래밍에 국한된 개념은 아니다.
- 한 번 계산된 결과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있다.
피보나치 수열
- 다이나믹 프로그래밍을 활용 가능한 문제중 가장 대표적인 문제라고 할 수 있다.


위와 같은 피보나치 수열에서 단순한 재귀를 활용 하여 푼다면 아래와 같이 작성된다.
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(4))하지만 이런식으로 풀게되면 반복 호출이 계속되기 때문에 지수의 시간 복잡도를 가지게 된다.
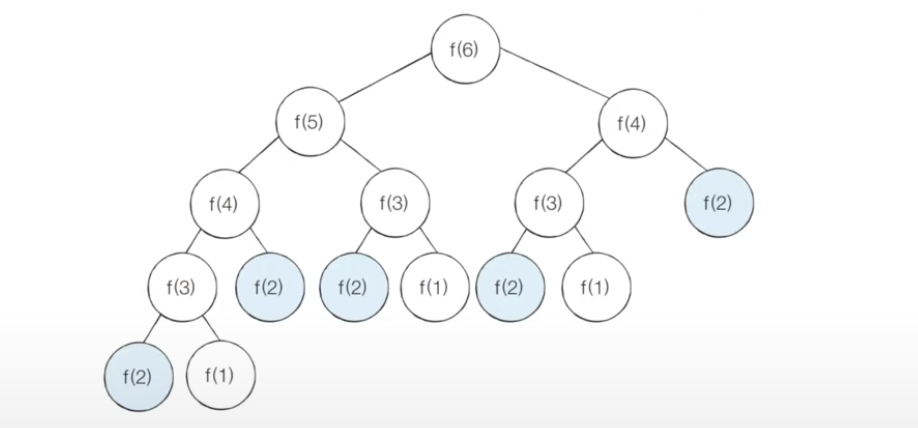
위와 같이 f(2)가 여러번 반복되어 호출되는 것을 볼 수있다.
빅오 표기법을 기준으로 : O(2^N)의 시간복잡도를 가지게 되는데, f(30)만 계산해도 10억가량이다.
f(100)을 계산하려면 1뒤에 0이 30개가 넘는다..
이러한 방법을 해결하기 위해선 중복된 반복 호출을 해결할 수 있는 다이나믹 프로그래밍을 사용하는 것이다.
피보나치 수열은 아까 위에서 작성한 다이나믹 프로그래밍 사용 조건 두가지를 모두 만족한다.
다이나믹 프로그래밍을 이용한 bottom-up형식으로 피보나치 수열을 만들어보자.
# DP 테이블 초기화
d = [0] * 100
# 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1
d[2] = 1
n = 99
# 피보나치 함수를 반복문으로 구현(bottom-up 다이나믹 프로그래밍)
for i in range(3, n+1):
d[i] = d[i-1] + d[i-2]
print(d[n])위와 같이 작성하면 메모이제이션을 이용하여 아래와 같은 색칠 된 노드만 처리가 되고, 반복된 호출을 줄일 수 있다.

'알고리즘' 카테고리의 다른 글
| Dynamic Programming #3 (문제풀이 2) (0) | 2023.10.11 |
|---|---|
| Dynamic Programming #2 (문제풀이 1) (0) | 2023.10.09 |
| 백준 1918 (후위 표기식) (0) | 2023.08.17 |
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
목차

이번 문제는 Stack을 이용해 풀어볼 것이다.
1. 피연산자는 스택에 넣지 않고 바로 출력을 할 것이고, 연산자는 우선순위가 존재하므로 스택에 넣어 순서에 맞게 출력을 해보자
2. '(' 일때는 일단 스택에 집어넣자.
3. '+' or '-' 일때는 연산자 중에 가장 낮은 우선순위므로 현재 스택에 있는 연산자들을 먼저 뽑아낸 후 스택에 집어넣어 준다. '(' top가 '(' 일때는 우선순위가 변경되므로 예외처리를 해줘야한다.
4. '*' or '/' 일때는 괄호 안에 있는 연산자를 제외하고 가장 높은 우선순위를 가지므로 top이 이와 같은 우선순위를 가진다면 먼저 뽑아낸 뒤 스택에 넣자.
5. ')' 일때는 짝에 맞는 '('이 나올때까지 가장 높은 우선순위를 가지는 연산자이므로 뽑아낸다. 그리고 스택에 남은 '('는 pop해서 없애주자.
6. 표기식은 대문자 'A'~'Z'로 지정해준다.
7. 이후에 스택에 남아있는 연산자들을 뽑아낸다.
import sys
my_input = sys.stdin.readline()
my_stack = []
for char in my_input:
if char == '(':
my_stack.append(char)
if char in ['+', '-']:
while my_stack and my_stack[-1] != '(':
print(my_stack.pop(), end='')
my_stack.append(char)
if char in ['*', '/']:
while my_stack and my_stack[-1] != '(' and (my_stack[-1] == '*' or my_stack[-1] == '/'):
print(my_stack.pop(), end='')
my_stack.append(char)
if char == ')':
while my_stack and my_stack[-1] != '(':
print(my_stack.pop(), end='')
my_stack.pop()
if char >= 'A' and char <= 'Z':
print(char , end='')
while my_stack:
print(my_stack.pop(), end = '')
'알고리즘' 카테고리의 다른 글
| Dynamic Programming #2 (문제풀이 1) (0) | 2023.10.09 |
|---|---|
| Dynamic Programming #1 (0) | 2023.10.09 |
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
| 백준 11657(타임머신) (0) | 2023.08.03 |
목차
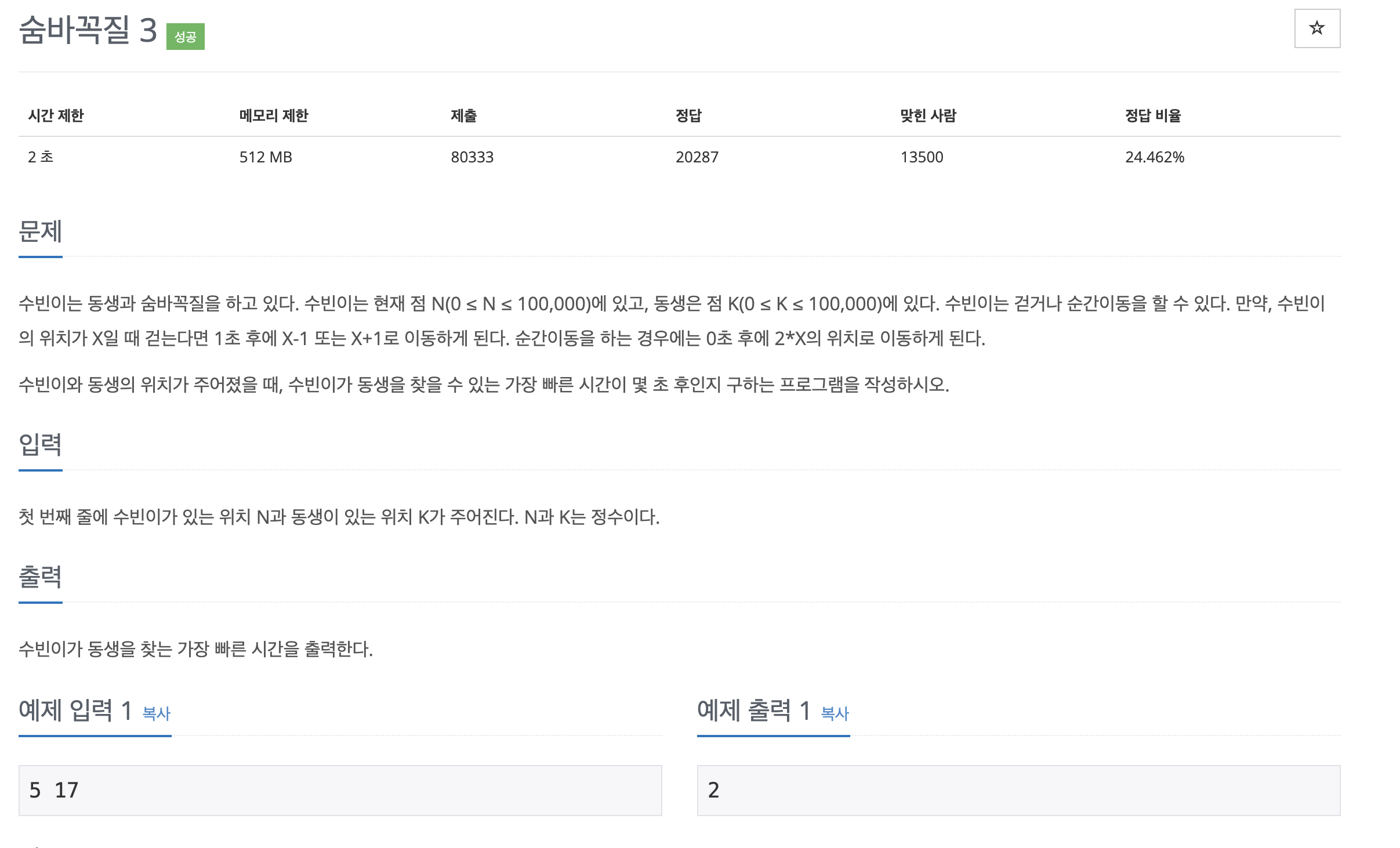
이번 문제는 최단거리를 구하는 문제 중 하나이므로 다익스트라를 사용해도 되고, BFS를 사용해도 될 거 같다.
BFS의 시간 복잡도는 O(V+E) 이고,
다익스트라의 시간 복잡도는 O(ElogV) 이므로
효율이 더 좋은 BFS를 사용해 볼 것이다.
import sys
from collections import deque
input = sys.stdin.readline
def BFS():
q = deque()
q.append(N)
while q:
x = q.popleft()
if x == K:
print(visited[x])
break
for i in (x-1, x+1, x*2):
if 0 <= i <= max and visited[i] == -1: # i가 0 ~ max 사이의 값이고, 방문하지 않은 노드일 경우에만 방문
if i == x*2 and i > 0:
visited[i] = visited[x]
q.appendleft(i) # 순간이동 한 노드는 높은 우선순위
else:
visited[i] = visited[x] +1
q.append(i)
max = 100000
N, K = map(int, input().split())
visited = [-1] * (max + 1)
visited[N] = 0
BFS()
'알고리즘' 카테고리의 다른 글
| Dynamic Programming #1 (0) | 2023.10.09 |
|---|---|
| 백준 1918 (후위 표기식) (0) | 2023.08.17 |
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
| 백준 11657(타임머신) (0) | 2023.08.03 |
| Attack Range (ALGORITHM JOBS) (0) | 2023.07.29 |
목차

이번에 풀어 볼 문제는 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)에 관한 기본적이면서 중요한 문제이다.
DFS는 재귀를 이용하여 풀고, BFS는 deque를 이용하여 풀어볼 것이다.
방문 여부를 판별하는 boolean 형식의 visited를 두어 중복 방문을 방지하고,
타겟 노드와 연결되어 있는지에 대한 부분도 boolean 형식을 이용할 것이다. (간선이 양방향이므로 양쪽 모두 변경하자)
from collections import deque
def BFS(V):
q = deque([V])
visited2[V] = True # 첫 시작점은 방문 True로 초기화
while q:
V = q.popleft()
print(V, end=" ")
for i in range(1, N + 1):
if not visited2[i] and graph[V][i]: # 방문 했던 곳이 아니고, V 값과 연결되어 있는지
q.append(i)
visited2[i] = True # 방문(True)으로 초기화
def DFS(V):
visited1[V] = True
print(V, end=" ")
for i in range(1, N + 1):
if not visited1[i] and graph[V][i]: # 방문 했던 곳이 아니고, V 값과 연결되어 있는지
DFS(i) # 재귀 호출을 이용하여 깊은 탐색
N, M, V = map(int, input().split())
graph = [[False] * (N + 1) for _ in range(N + 1)]
for _ in range(M): # 노드끼리의 연결 유무(양방향이므로 둘 다 True로 설정)
a, b = map(int, input().split())
graph[a][b] = True
graph[b][a] = True
visited1 = [False] * (N + 1) # DFS 방문 유무
visited2 = [False] * (N + 1) # BFS 방문 유무
DFS(V)
print()
BFS(V)
'알고리즘' 카테고리의 다른 글
| 백준 1918 (후위 표기식) (0) | 2023.08.17 |
|---|---|
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
| 백준 11657(타임머신) (0) | 2023.08.03 |
| Attack Range (ALGORITHM JOBS) (0) | 2023.07.29 |
| 점수 계산 (ALGORITHM JOBS) (0) | 2023.07.29 |
목차


문제를 보면 최단거리 구하는 문제인걸 바로 알 수 있다.
최단거리 알고리즘인 세가지를 생각해 볼 수 있다.
1. 다익스트라(Dijkstra)
2. 벨만-포드(Bellman-Ford)
3. 플로이드-워셜(Floyd-Warshall)
시작점이 정해져 있으니 다익스트라(Dijkstra), 벨만-포드(Bellman-Ford)중에 하나를 사용하면 되고, 조건에서 보면 C<0인 경우도 다루고 있기때문에 가중치가 음수일때 사용하는 벨만-포드(Bellman-Ford)를 사용하면 된다.
문제는 벨만-포드(Bellman-Ford)알고리즘를 이용해서 음의 사이클이 존재하는가를 확인하면 된다.
(노드 개수-1)까지 반복하면 모든 노드는 최단거리로 연결이 되고, 이후에 한번 더 반복 비교를 했을때 가중치가 update되면 음의 사이클이 존재한다고 볼 수 있다.
import sys
input = sys.stdin.readline
N, M = map(int, input().split()) # N(노드 개수) M(에지 개수)
edges = [] # 에지 정보 저장 리스트
distance = [sys.maxsize] * (N+1) # 거리 리스트(충분히 큰 수로 저장한다.)
#distance의 길이를 N+1까지 저장하여 index 1부터 시작하도록 한다.
for i in range(M):
start, end, time = map(int, input().split())
edges.append((start, end, time))
distance[1] = 0 # 시작점은 0으로 초기화
for _ in range(N-1):
for start, end, time in edges:
if distance[start] != sys.maxsize and distance[end] > distance[start] + time:
distance[end] = distance[start] + time
# 출발노드가 무한대가 아니고 종료 노드 값 < 출발 노드 값 + 에지 가중치일때
# distance[end] 값을 출발 노드 값 + 에지 가중치로 변경해준다.
mCycle = False # 음의 사이클 여부
for start, end, time in edges:
if distance[start] != sys.maxsize and distance[end] > distance[start] + time:
mCycle = True
# N-1까지 반복한 후에 한번 더 반복 했을때 update가 된다면 음의 사이클이 존재한다.
if not mCycle:
for i in range(2, N+1):
if distance[i] != sys.maxsize:
print(distance[i])
else:
print(-1)
else:
print(-1)
'알고리즘' 카테고리의 다른 글
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
|---|---|
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
| Attack Range (ALGORITHM JOBS) (0) | 2023.07.29 |
| 점수 계산 (ALGORITHM JOBS) (0) | 2023.07.29 |
| 백준 17298(오큰수) (0) | 2023.07.29 |
목차

(1) (i,j) ~ (x,y) 까지 거리를 구한다.
(2) 이 거리가 R안에 들어오는가??
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int X = sc.nextInt();
int Y = sc.nextInt();
int R = sc.nextInt(); //사거리
int arr[][] = new int[105][105];
for(int i = 1 ; i<=N ; i++){
for(int j = 1; j<=N ; j++){
int a = X-i;
int b = Y-j;
if(a<0)a*=-1; // 단순 거리 계산이기 때문에 부호를 변경해야함
if(b<0)b*=-1; // 단순 거리 계산이기 때문에 부호를 변경해야함
int dist = a+b;
if(dist==0)arr[i][j]=-1;
else if(dist<=R)arr[i][j]=dist;
}
}
for(int i = 1 ; i<=N ; i++){
for(int j = 1; j<=N ; j++){
if(arr[i][j]==-1) System.out.print("x ");
else System.out.print(arr[i][j]+" ");
}
System.out.println();
}
// Please Enter Your Code Here
}
}입력
8
4 5 3출력
0 0 0 0 3 0 0 0
0 0 0 3 2 3 0 0
0 0 3 2 1 2 3 0
0 3 2 1 x 1 2 3
0 0 3 2 1 2 3 0
0 0 0 3 2 3 0 0
0 0 0 0 3 0 0 0
0 0 0 0 0 0 0 08x8 크기의 형태로, (4,5)위치의 플레이어 x값에 사거리가 3인 x
x를 기준으로 가로, 세로 길이 합이 3인 좌표들을 구해야한다.
a+b의 값을 dist에 집어넣고 dist가 0이라면 그 좌표는 플레이어 x의 좌표이다.
arr은 int형이므로 x의 좌표에 "x"를 넣지 못하므로 -1을 넣는다.
이 후에 -1 값을 "x"로 출력한다.
'알고리즘' 카테고리의 다른 글
| 백준 13549 (숨바꼭질 3) (0) | 2023.08.11 |
|---|---|
| 백준 1260(DFS와 BFS) (0) | 2023.08.07 |
| 백준 11657(타임머신) (0) | 2023.08.03 |
| 점수 계산 (ALGORITHM JOBS) (0) | 2023.07.29 |
| 백준 17298(오큰수) (0) | 2023.07.29 |








